Es correcto decir que si un avión no se accidentó nunca en 1000 vuelos, la probabilidad de accidente es cero?

NO, No es correcto. Este razonamiento tiene algunas fallas importantes:
Tamaño de la muestra: 1000 vuelos es una muestra relativamente pequeña en comparación con la cantidad total de vuelos que un avión realiza durante su vida útil.
Falacia del jugador: Asumir que porque algo no ha ocurrido en el pasado, no ocurrirá en el futuro.
Factores variables: Las condiciones de cada vuelo pueden variar, y factores como el mantenimiento, el clima o el error humano podrían aumentar el riesgo en cualquier momento.
Los aviones comerciales tienen una probabilidad de accidente de 1 en 2 millones. En el caso del Concord, después de 70.000 vuelos sin accidentes, se convirtió en el avión más seguro del mundo. Esto hasta que ocurrió en el 70.001 y pasó a ser el más inseguro del mundo.
Esta no es, claramente, una estimación robusta.
Regla de tres o Regla del tres
Esta regla proporciona una estimación conservadora del límite superior de la probabilidad de un evento que no ha ocurrido en una serie de pruebas.
La fórmula es:
P ≈ 3 / n
Donde: P = probabilidad máxima estimada del evento n = número de pruebas (en este caso, vuelos)
Aplicando esta regla a nuestro ejemplo:
P ≈ 3 / 1000 = 0.003 = 0.3%
Esto sugiere que, con un 95% de confianza, la probabilidad máxima de un accidente no es cero, sino aproximadamente 0.3% o menos.
Es importante notar que esta es una estimación conservadora del límite superior. La probabilidad real podría ser mucho menor, pero no tenemos suficiente información para afirmar que es exactamente cero.
Corrección de Laplace o la Regla de Sucesión de Laplace
Esta corrección es especialmente útil cuando se trata de eventos raros o que no han ocurrido en una serie de pruebas.
La Corrección de Laplace aborda algunas limitaciones de la estimación de probabilidad basada únicamente en la frecuencia observada. Aquí están los detalles principales:
Fórmula de la Corrección de Laplace: P = (s + 1) / (n + 2) Donde: P = probabilidad estimada s = número de éxitos (en este caso, accidentes) n = número total de pruebas (en este caso, vuelos)
Aplicación al ejemplo del avión: En el caso de 0 accidentes en 1000 vuelos: P = (0 + 1) / (1000 + 2) ≈ 0.000998 ≈ 0.1%
Ventajas de la Corrección de Laplace
Evita probabilidades de 0 o 1, que a menudo son poco realistas.
Proporciona una estimación más conservadora que la simple frecuencia relativa.
Es especialmente útil para muestras pequeñas o eventos raros.
Interpretación: La Corrección de Laplace sugiere que, incluso sin observar ningún accidente en 1000 vuelos, deberíamos estimar una pequeña probabilidad de accidente (aproximadamente 0.1% en este caso) en lugar de asumir que es cero.
Comparación con la Regla de Tres: La Corrección de Laplace tiende a dar una estimación más baja que la Regla de Tres para eventos que no han ocurrido, lo que la hace menos conservadora pero potencialmente más precisa en muchos casos.
Esta corrección refleja el principio de que, en ausencia de información completa, es prudente asumir una pequeña posibilidad de que el evento ocurra, incluso si no se ha observado en las pruebas realizadas.
Otros métodos
Estimador de Good-Turing: Esta técnica se usa comúnmente en procesamiento del lenguaje natural, pero también puede aplicarse a otros campos.
P(unseen) ≈ N1 / N
Donde: N1 = número de eventos que ocurrieron exactamente una vez N = número total de observaciones
Intervalo de confianza de Hanley-Lippman-Hand: Proporciona un intervalo de confianza para la probabilidad de un evento que no ha ocurrido.
Límite superior del IC del 95% ≈ 1 – (0.05)^(1/n)
Donde n es el número de pruebas.
Estimador de máxima verosimilitud con suavizado: Similar a la corrección de Laplace, pero permite ajustar el grado de suavizado.
P = (s + α) / (n + αk)
Donde: s = número de éxitos n = número total de pruebas α = parámetro de suavizado (α = 1 es equivalente a la corrección de Laplace) k = número de posibles resultados
Estimación bayesiana: Utiliza distribuciones de probabilidad previas y posteriores.
P = (s + αp) / (n + α)
Donde: p = probabilidad previa α = peso dado a la probabilidad previa
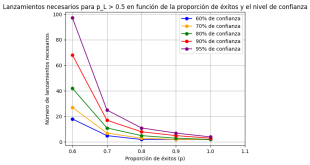
Método de Wilson para intervalos de confianza: Proporciona intervalos de confianza más precisos para proporciones, especialmente con muestras pequeñas o proporciones cercanas a 0 o 1.
Cada una de estas fórmulas tiene sus propias ventajas y se aplica mejor en diferentes contextos. La elección depende de factores como el tamaño de la muestra, el dominio específico del problema y las suposiciones que estemos dispuestos a hacer sobre la distribución subyacente.
Condiciones de aplicación de cada método
Regla de Tres
Tamaño de muestra: Pequeño a mediano (hasta unos miles de observaciones)
Dominio ideal: Seguridad, control de calidad
Ejemplo: Estimar el riesgo máximo de un efecto adverso raro en un medicamento
Suposiciones: Distribución binomial, eventos independientes
Cuándo usar: Cuando se necesita una estimación conservadora del límite superior de probabilidad
Corrección de Laplace
Tamaño de muestra: Pequeño a mediano
Dominio ideal: Clasificación de textos, análisis de riesgos
Ejemplo: Estimar la probabilidad de palabras no vistas en un corpus lingüístico
Suposiciones: Distribución uniforme previa
Cuándo usar: Cuando se quiere evitar probabilidades de 0 en eventos no observados
Estimador de Good-Turing
Tamaño de muestra: Mediano a grande
Dominio ideal: Procesamiento del lenguaje natural, ecología
Ejemplo: Estimar la probabilidad de especies no observadas en un ecosistema
Suposiciones: La frecuencia de eventos raros sigue un patrón predecible
Cuándo usar: Cuando hay muchos eventos únicos o raros en los datos
Intervalo de confianza de Hanley-Lippman-Hand
Tamaño de muestra: Pequeño a mediano
Dominio ideal: Epidemiología, pruebas clínicas
Ejemplo: Estimar el límite superior de riesgo de una complicación rara en una cirugía
Suposiciones: Distribución binomial
Cuándo usar: Cuando se necesita un intervalo de confianza para eventos no ocurridos
Estimador de máxima verosimilitud con suavizado
Tamaño de muestra: Variable, desde pequeño a grande
Dominio ideal: Aprendizaje automático, procesamiento de señales
Ejemplo: Suavizar estimaciones de probabilidad en un modelo de lenguaje
Suposiciones: La intensidad del suavizado puede ajustarse según el conocimiento previo
Cuándo usar: Cuando se quiere un balance entre los datos observados y una distribución previa
Estimación bayesiana
Tamaño de muestra: Cualquier tamaño, especialmente útil para muestras pequeñas
Dominio ideal: Finanzas, medicina personalizada
Ejemplo: Actualizar la probabilidad de éxito de un tratamiento basado en nuevos datos clínicos
Suposiciones: Se dispone de una distribución previa informativa
Cuándo usar: Cuando se tiene información previa confiable y se quiere incorporar a la estimación
Método de Wilson para intervalos de confianza
Tamaño de muestra: Pequeño a mediano, especialmente útil para muestras pequeñas
Dominio ideal: Encuestas de opinión, estudios de mercado
Ejemplo: Calcular intervalos de confianza para la proporción de votos en una elección con pocos votantes
Suposiciones: Distribución binomial, pero funciona bien incluso cuando la aproximación normal no es adecuada
Cuándo usar: Para calcular intervalos de confianza más precisos en proporciones, especialmente cerca de 0 o 1
Otros métodos estadísticos complementarios
1. Distribución Beta-Binomial (Bayesiano)
Es una extensión del enfoque bayesiano mencionado, utilizando una distribución Beta como una distribución previa. Este método es útil cuando se desea modelar una probabilidad con incertidumbre basada en observaciones previas.
Ventajas:
- Permite ajustar el modelo con una mayor flexibilidad mediante la selección de α\alphaα y β\betaβ, dependiendo de las observaciones anteriores.
- Apropiado cuando tienes cierta información previa sobre la tasa de éxito.
2. Estimadores no paramétricos
Métodos no paramétricos como bootstraping pueden proporcionar una estimación empírica de la distribución de probabilidad del evento basado en remuestreos de los datos observados.
Ventajas:
- No requiere suposiciones específicas sobre la distribución subyacente.
- Útil cuando los modelos paramétricos (como la binomial o beta) no se ajustan bien a los datos.
3. Distribución de Poisson
Cuando el evento que se está estudiando es extremadamente raro, la distribución de Poisson es útil para modelar la ocurrencia de tales eventos en un número grande de pruebas.
Ventajas:
- Adecuada para modelar eventos raros en grandes muestras.
- Muy usada en contextos de fallos mecánicos y eventos catastróficos.
4. Método Jeffreys (Intervalo de Confianza Bayesiano)
Este método ofrece intervalos de confianza más precisos, particularmente cuando hay eventos raros o no observados. Utiliza un enfoque bayesiano con una distribución previa no informativa (Jeffreys prior).
Ventajas:
- Funciona mejor con muestras pequeñas en comparación con los intervalos de confianza estándar de Wilson o Wald.
- No depende de una aproximación normal.
5. Regla de Cromwell
Un principio importante en probabilidad bayesiana es evitar asignar probabilidades extremas de 0 o 1 a cualquier evento, incluso sin información previa. Este principio es una extensión de las ideas presentadas por la Corrección de Laplace, pero enfatiza que es irracional asignar certeza absoluta a cualquier evento, sobre todo si la muestra es limitada.
 Solo para Entendidos
Solo para Entendidos