Solo para Entendidos
Related Articles
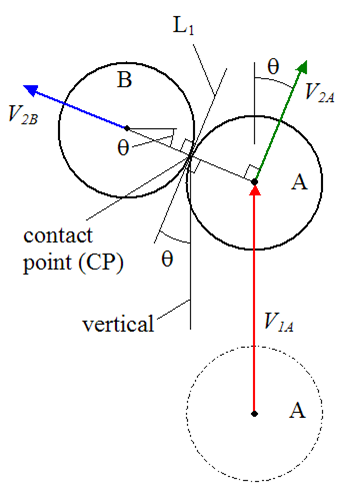
En las colisiones oblicuas en choques elásticos, la bola A se mueve en dirección a la B, que se encuentra en reposo, a una velocidad V1A .
Al colisionar, la bola A se desvía un ángulo θ hacia la derecha respecto de la línea de trayectoria (Rojo) con una velocidad V2A (Verde).
La bola B, después del impacto, sale con una velocidad V2B (Azul).
Al momento del impacto, el centro de cada bola definen una línea cuya perpendicular es el plano de contacto L1.
En la colisión de dos bolas se verifica la conservación de la cantidad de movimiento como así también la de energía siendo así un choque perfectamente elástico.
Nótese que en el caso del gráfico el cual se trata de dos bolas de la misma masa, el ángulo formado por los dos vectores velocidad resultantes después del impacto, forman un ángulo de 90 grados.
Tomando los ejes haciendo coincidir Y con V2B y X con V2A, se puede descomponer en ellos las cantidades de movimiento y se verifica que la bola A transfiere en su totalidad la energía a la B en el eje Y y nada en el X ya que el punto de contacto está sobre el plano X y no hay fuerzas en X, solo en Y. Por tanto la velocidad resultante de A (que solo va a tener componente en X) será igual a la que traía su componente en X antes del choque, es decir, V1A . cos θ.
Partiendo del caso genérico donde las masas puedan ser diferentes, las ecuaciones resultan:
(de la conservación de la cantidad de movimiento) m1 v1A = m1 v2A + m2 v2B
(al ser un choque elástico, se conserva la energía) ½ m1 v1A2 = ½ m1 v2A2 + ½ m2 v2B2
en cada eje: Px m1 v1A = m1 v2A cos θ + m2 v2B cos φ
Py 0 = m1 v2A sin θ – m2 v2B sin φ
Si m1 = m2 = m, entonces:
(de la conserva de la energía) ½ m v1A2 = ½ m v2A2 + ½ m v2B2
(dividiendo por m y multiplicando por 2) v1A2 = v2A2 + v2B2 [1]
en cada eje y reordenando: Px: v2B cos φ = v1A – v2A cos θ [2]
Py: v2B sin φ = v2A sin θ [3]
elevando al cuadrado: v2B2 cos2φ = (v1A – v2A cos θ)2
v2B2 sin2φ = v2A2 sin2θ
Sumando v2B2 (sin2φ + cos2φ) = v1A2 – 2 v1A v2A cos θ + v2A2 cos2θ + v2A2 sin2θ
v2B2 = v1A2 – 2 v1A v2A cos θ + v2A2
