En los años ‘20, Alexander Friedmann, sugieren que el universo nació de una “gran explosión” –big bang– en un estado muy denso y caliente el cual se viene expandiendo desde entonces. Las ecuaciones de Friedmann modelizan la dinámica de esta expansión según su densidad y geometría. Estas ecuaciones incluyen la constante de Hubble que muestra la tasa de expansión actual del universo. Es decir, el aumento de velocidad de los objetos de acuerdo a sus distancias.
Para definirla, se requiere de algunos parámetros los cuales se pueden obtener experimentalmente. H, la constante de Hubble, que define el ritmo de la expansión; Ωm, la densidad de masa del universo; y Ωk, la curvatura del universo. Las primeras mediciones se desarrollaron en 1929, año en que Edwin Hubble observó que el universo se expandía demostrando que cuanto más alejada de nosotros esté una galaxia, más rápido ésta se aleja de nosotros. A esta relación velocidad-distancia se la llama ley de Hubble. Se define así la tasa de expansión como H0. Este valor se lo calculó inicialmente en alrededor de 500 kilómetros por segundo por megapársec el cual no cerraba correctamente el modelo.
La precisión resultaba clave para desarrollar el modelo y establecer así edad y tamaño del universo. El Telescopio Espacial Hubble (TEH), puesto en órbita en 1990 tuvo como una de las principales razones para ser construido el estableces estos parámetros con mayor precisión.
Así es que el Key project del TEH, el cual llevó ocho años de trabajo y cerca de 1000 horas del tiempo del TEH, acabó en 2001 dejando un valor de H0 -constante de Hubble- que permitió modelizar con mayor precisión el universo.
La variable H0 debería ser sencilla de calcular observando las galaxias y midiendo sus corrimientos al rojo para así concluir en la velocidad de cada una de ellas. Pero tanto las velocidades, que se ven afectadas por las velocidades peculiares (velocidad propia de la galaxia NO atribuible a la expansión del universo), como la distancia, son difíciles de medir.
Cálculo de distancias para la determinación de la constante de Hubble
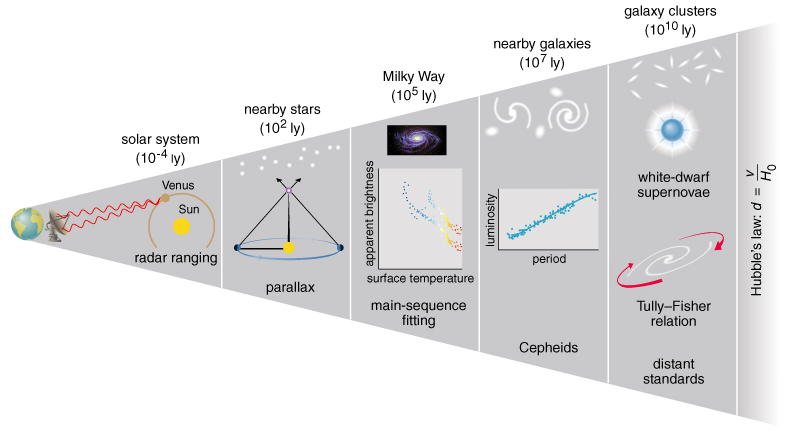
La dificultad de las distancias se resuelve en las galaxias cercanas por medio del paralaje, es decir, el cálculo trigonométrico de la distancia por la variación del ángulo de observación de la galaxia desde un extremo a otro de la órbita terrestre. Para objetos más distantes, el método se basa en el cálculo de la distancia necesaria para que un objeto de brillo conocido se vea con determinada magnitud en la Tierra.
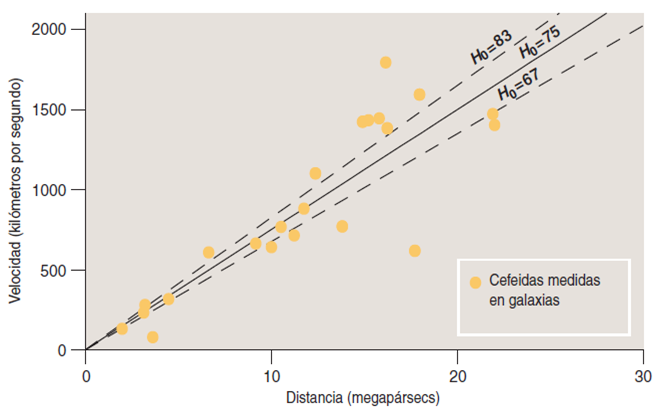
Las estrellas Cefeidas, pulsan con períodos de entre 2 y 100 días y tienen una relación entre su brillo intrínseco y la frecuencia de pulsación, por lo que se utilizan como standard candles. Estas estrellas se pueden medir con precisión hasta unos 30 mega pársecs. (también ver relación Faber-Jackson)
Para ir más allá de los 30 mega parsecs, existen otros métodos como –por ejemplo- la relación Tully-Fisher que establece que la velocidad rotacional de una galaxia espiral está relacionada con su luminosidad. Las más brillantes giran más rápido que las débiles. Existe una relación similar para las galaxias elípticas y como último, el conteo de estrellas por pixel donde una galaxia cercana parece granulosa y una distante, más difusa. Estos métodos son aplicables a distancias de hasta 150 mega parsecs.
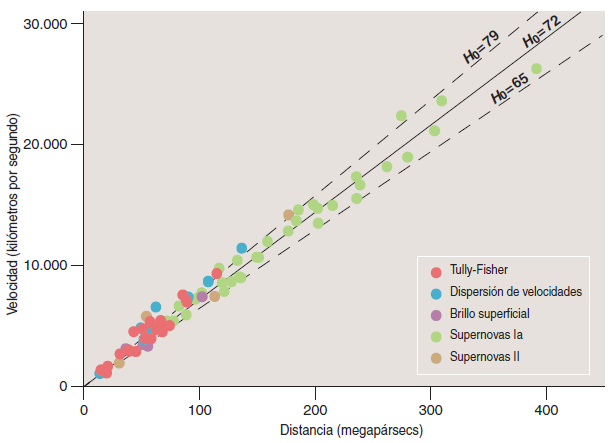
Más allá de esas distancias, las candelas estándar utilizadas son los objetos más luminosos del universo, las supernovas. Entre ellas, la de tipo Ia que estalla cuando una enana blanca aumenta su masa debido a la cercanía de otra estrella yendo por encima del límite de Chandrasekhar (1.4 Masa del Sol) llegando al colapso gravitatorio. Esta irradiará como una galaxia entera por un período de tiempo permitiendo calcular distancias hasta con velocidades de recesión de 30.000 km/s (la décima parte de la velocidad de la luz) donde las velocidades peculiares de 200 a 300 km/s no son representativas. Así podemos calcular distancias de hasta 400 mega parsecs.
Existe un alto grado de coincidencia en el valor de H0 que resulta del cálculo según los diferentes métodos: las Cefeidas 75; supernovas tipo Ia, 71; relación de Tully-Fisher, 71; dispersión de velocidades en galaxias elípticas, 82; fluctuaciones de brillo superficial, 70; y las supernovas de tipo II, 72. Una media ponderada de estos valores da un resultado para la constante de Hubble de este momento H0 = 72.
Métodos de determinación de distancias en función de la lejanía
 Solo para Entendidos
Solo para Entendidos