Árboles de Decisión – Machine Learning

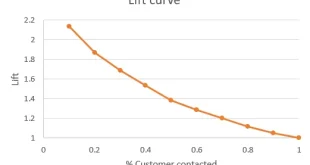
Los árboles de decisión intentan ofrecer una manera simple de catalogar donde a través de la menor cantidad de preguntas posibles, identificar un ítem con una clase determinada.

Idealmente los atributos que conforman los nodos del árbol, deben generar partes “puras” donde dividan completamente las clases.

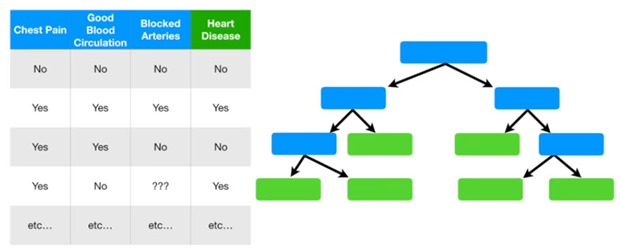
Por ejemplo pensemos en un set con información sobre enfermedades del corazón con la siguiente información donde los atributos son síntomas que clasifican a un paciente entre los que están enfermos del corazón o no.

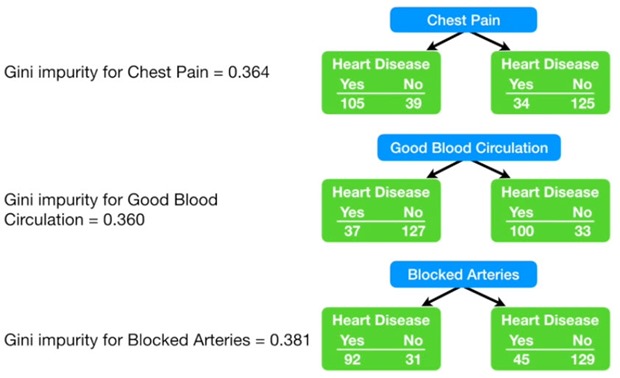
Contando cuántos hay con cada síntoma en cada grupo de “enfermo”, “no enfermo”, construimos esto donde se ve que ningún síntoma es contundente con un 100%. Es decir que ninguno genera hojas “puras”.

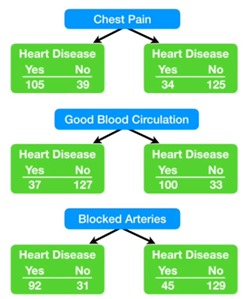Con dolor de pecho: 105 Si, 39 No
Sin dolor de pecho: 34 Sí, 125 No

Con buena circulación: 37 Sí, 127 No
Sin buena circulación: 100 Sí, 33 No

Con arterias bloqueadas: 92 Sí, 31 No
Sin arterias bloqueadas: 45 Sí, 129 No

Para determinar por qué criterio empezar a partir en ramas el árbol, se debe poder disponer de una medida de impureza.

Es así que hay tres criterios para elegir el nodo sobre el cual partir el árbol. Todos ellos tienen como finalidad, lograr el árbol más compacto posible con las ramas más puras al inicio.

Árboles de Desición – Gini

Para calcular el grado de impureza de “dolor de pecho”, se calcua:

1 – (probabilidad de Sí)² – (probabilidad de No)²

resultando,

1 – (105/(105+39))² – (39/(105+39))² = 0.395

1 – (34/(34+125))² – (125/(34+125))² = 0.336

El coeficiente final será la suma de ambos pero, como cada hoja representa distinto número de pacientes (144 y 159 en cada caso), se debe hacer el promedio ponderado de cada uno de estos resultados.

0.395 . (144/144+159) + 0.336 . (159/144+159) = 0.364

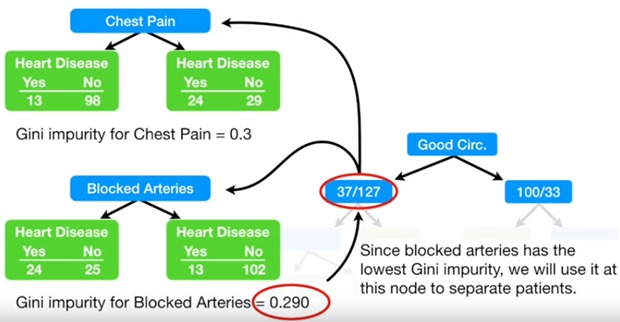
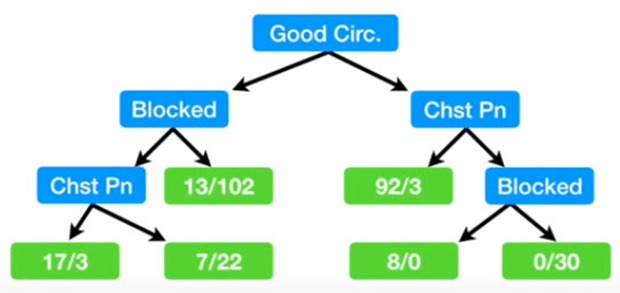
Se ve entonces que el menor índice es para “Buena Circulación”. Una vez generado los nuevos nodos, hay que aplicar el mismo método para ver cuál de los criterios es más adecuado.  El proceso se detiene si lo que se produce tiene mayor impureza de lo que se tenía antes.

En el caso de tratarse de un atributo numérico, se ordenan los datos y se calculan los promedios de los datos adyacentes calculando el coeficiente de impureza Gini para cada uno de estos promedios. De esta manera se elige el valor pivote a utilizar par en nodo.

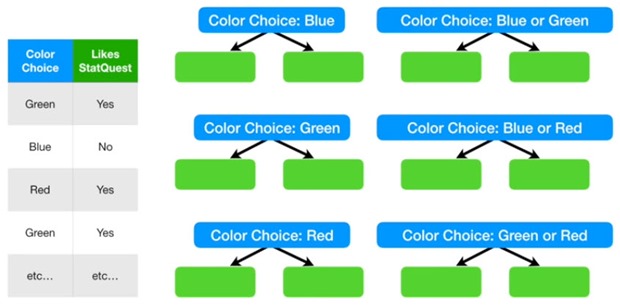
En el caso de tratarse de un grupo de posibilidades discretas como colores, el cálculo del menor gini se deberá hacer sobre las posibilidades.

Árboles de Desición – Entropía

Para lograr estos Pure Nodes, se usa la teoría de la información de Claude Shannon donde se habla de entropía (desorden), que evalúa el atributo según la cantidad de información que gana al hacer el split utilizando ese atributo como nodo y no otro.

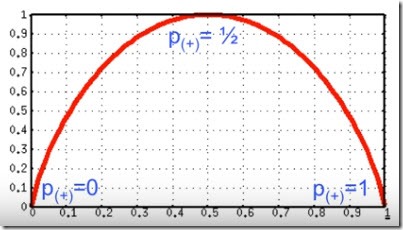
H = –p(+) log₂ p(+) –p(-) log₂ p(-)

donde p son los porcentajes de positivos o negativos. Por ejemplo, si tenemos un nodo con 3 si y 3 no

H = –3/6 log₂(3/6) – 3/6 log₂(3/6) = 1 bit (peor de los casos)

Si por el contrario tenemos un nodo puro con x ej, 4 si y 0 no

H = –4/4 log₂(4/4) – 0/4 log₂(0/4) = 0 bit (peor de los casos)

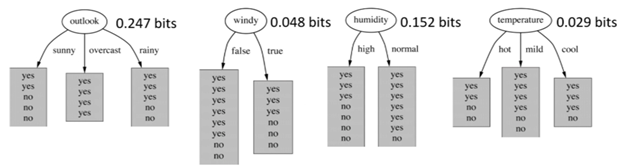
Ejemplo de la base de Weather que viene con el Weka.

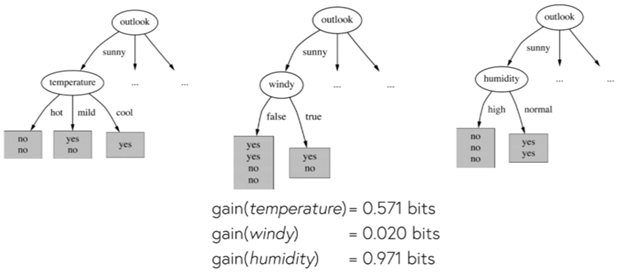
Así entonces elegimos el
Outlook y debemos hacer una nueva pregunta según otro atributo.

Árboles de Desición – Pureza