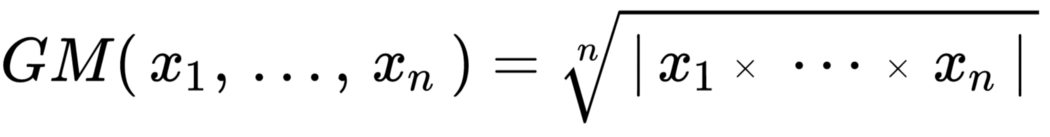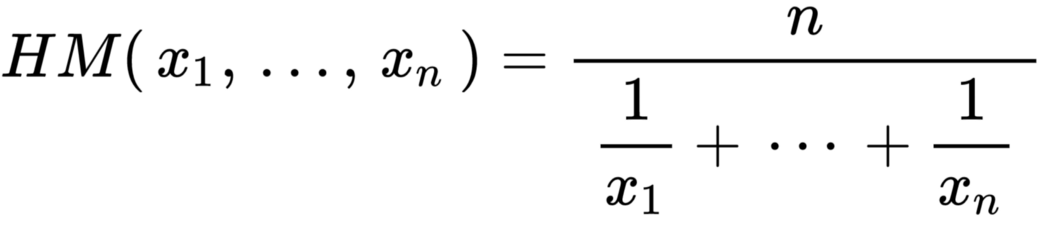La media aritmética es solo una de tres Medias Pitagóricas. También tenemos la geométrica y la harmónica.
La media aritmética es el promedio generado de la suma de los valores sobre la cantidad de ellos.
La media geométrica, surge de la multiplicación de los mismos y traídos a la escala original mediante la raíz n-ésima siendo n la cantidad de puntos.
Un ejemplo de esto es hallar la tasa promedio durante varios años siendo estos 1.01, 1.09, 1.06, 1.02, 1.15
(1.01 * 1.09 * 1.06 * 1.02 * 1.15)^(1/5) = 1.0648 (mientras el promedio da 1.066)
finalmente $100.000 * (1.06485-1) = 36,883.70 – resultado correcto.
Otro ejemplo es la comparación de medidas de diferentes escalas.
Local A
fuente1: rating 4.5
fuente2: rating 68
Local B
fuente1: rating 3
fuente2: rating 75
Las fuentes tienen escalas diferentes y sacando un promedio de cada uno no resultan métricas comparables (36.25 vs 39).
Mediante el media geométrica, sqr(4.5 * 68) = 17.5; sqr(3 * 75) = 15
La media armónica, resulta del promedio de los recíprocos a los cuales se los trae con el recíproco del resultado.
Un ejemplo es el cálculo de velocidad promedio de un vehículo que recorre un trayecto de 5 km a 30km/h a la ida y a 10 km/h a la vuelta.
Mediante la media harmónica, 1/(1/30 + 1/10) = 15
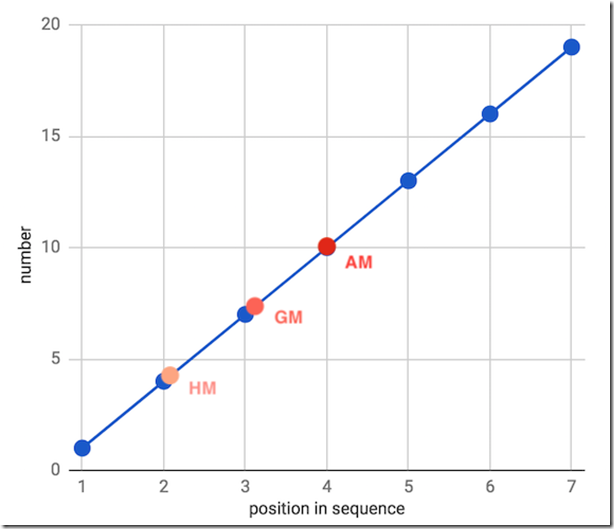
Copmparación. Sobre un mismo dataset.
Dataset {1, 4, 7, 10, 13, 16, 19…}
Finalmente, HM < GM < AM a menos que el dataset sea de un solo punto.
 Solo para Entendidos
Solo para Entendidos