Solo para Entendidos
Related Articles
Para la determinación de la densidad de un planeta, primero definamos densidad ρ como la masa sobre el volumen.
Según las leyes de Kepler, el período orbital de un satélite es proporcional a R³ e inversamente proporcional a a³ (semi eje mayor) y para que éste orbite, la Fuerza gravitatoria debe estar en equilibrio con la centrípeta entonces:
F = G.M.m/r² = m.v²/r ; P = 2.π.r/v
donde v es la velocidad radial, r la distancia del satélite al centro del planeta, G la constante gravitatoria, M la masa del planeta y P el período de translación alrededor del planeta.
substituimos la velocidad tangencial por el equivalente de 2.π.r/P resultando:
G.M.m/r² = (2.π.r/P)². m/r las m (masa del satélite) se cancelan a ambos lados
P².G.M = 4.π².r³ ratificando la ley de Kepler de proporcionalidad
M = (4.π²/G).r³/P² (4.π²/G) es constante (coeficiente de proporcionalidad)
Por tal, midiendo el radio de la órbita del planeta y midiendo el período, se puede establecer la masa.
G, constante gravitatoria, fue determinada con una precisión de un 99% por Cavendish en 1797 mediante un péndulo de torque.
El radio de la órbita del satélite del planeta en cuestión no se conoce, solo la distancia angular observable desde la Tierra. Para conocer la distancia, se necesita conocer la distancia al planeta.
Por la medición de los períodos orbitales planetarios se puede definir la distancia al sol en unidades relativas a la Tierra, es decir, la distancia –de por ejemplo Júpiter- al Sol es de 5.2 AU.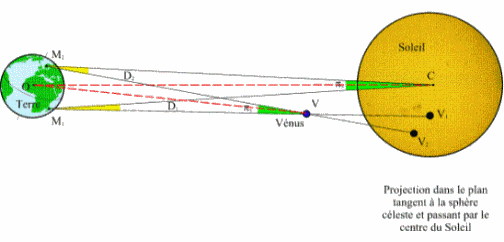 
La distancia de la Tierra al Sol fue determinada con precisión durante la Transición de Venus delante del Sol. Un observador en un extremo de la Tierra otro en el extremo opuesto, ven el comienzo o final del tránsito a diferente tiempo. Esta diferencia de 4 minutos hace que calculando la velocidad orbital de Venus a 0.72 AU y sabiendo que el radio de la Tierra es de 12.700 km, se pueda calcular AU. 1.5.10^8 km. Método propuesto por Halley. Otros métodos.
Así sabiendo AU, la distancia al planeta y por tanto su diámetro (volumen), la distancia al satélite y así su masa mediante el período del satélite; se puede calcular la densidad del mismo.
