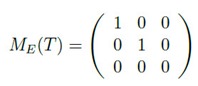Solo para Entendidos
Related Articles
Esta técnica tiene como finalidad encontrar una transformación de datos que permita reducir la dimensión del problema eliminando información redundante y a la vez explicar la mayor varianza de los datos para poder utilizarlos con distintas finalidades. Permitirá eventualmente visualizar la información multidimensional y explorar variables latentes.
Una recta define un espacio de dimensión 1 donde los puntos sobre ella se pueden definir mediante su distancia al centro de coordenadas, el cero. Dos rectas, pueden definir la posición de un punto cualquiera, en el plano que definen, siempre y cuando estas rectas se crucen, es decir, que no sean paralelas R2. En 3 dimensiones será lo mismo, R3, como así también en más dimensiones. Así, los clásicos ejes cartesianos ortogonales (producto escalar cero) y de módulo 1 (i, j, k), se los denominan canónicos. Este conjunto de vectores que generan un espacio vectorial de una dimensión dada, se llaman base.
A los puntos representados en el espacio sobre los ejes canónicos, se les puede aplicar transformaciones como proyecciones y rotaciones, Las transformaciones lineales que proyectan puntos sobre un eje determinado se denominan proyectores y cumplen con que al aplicarse más de una vez, no modifican el resultado (las nuevas coordenadas).
Por ejemplo, la matriz de transformación que proyecta, proyector, sobre el plano XY, donde Z=0, pasando de R3 a R2, es la siguiente:
Dada una transformación lineal T : Rn->Rn de un espacio en sí mismo, se dice que v ϵ Rn – {0} es un autovector asociado al autovalor λ ϵ R si se verifica que
T(v) = λ v
Matricialmente
A vt = λ v t
o
(A – λ I) vt = 0
donde I es la mat. Identidad, o sea
det (A – λ I) = 0
de la resolución de la última ec. resulta el polinomio característico de la matriz cuyas raíces son los autovalores.
Por ejemplo:
Así como el tamaño de un vector es caracterizado por el módulo, el de una matriz, está asociado a sus autovalores. Una medición es la traza que es la suma de la diagonal, o sus autovalores tr(A). Otra es mediante su determinante det(A) que resulta el producto de los autovalores. Ambas dan una noción de la variabilidad del conjunto.
Dicho esto, la intención es, dado un conjunto de puntos, encontrar la transformación que maximice la variabilidad en uno de sus nuevos ejes y de esta forma, de la matriz de varianza y covarianza que están asociadas con los autovalores que representan su tamaño.
Encontrar entonces una transformación donde el valor de los datos tenga mayor variabilidad permitiéndome poder prescindir eventualmente de alguna dimensión para poder explicar la mayoría se su varianza y lograr de esta manera una reducción dimensional.
Hotelling lo planteó desde la búsqueda de la combinación lineal de las variables que maximicen la variabilidad.
Pearson, el subespacio de mejor ajuste por el método de mínimos cuadrados minimizando la suma de cuadrados de las distancias de cada punto al subespacio de representación.
Gower, minimizando la discrepancia entre las distancias euclídeas entre los puntos calculados en el espacio original y en el subespacio de proyección que son las coordenadas principales.
La aplicación de PCA tiene sentido cuando existen correlaciones entre las variables lo cual nos permite de alguna forma poder prescindir de alguna de ellas. Si todas las variables aportan a la varianza de igual manera, las componentes principales van a ser similares y no se va a lograr explicar gran porcentaje de la variabilidad con solo algunas de ellas.
Es recomendable basar el análisis sobre la matriz de correlación ya que no se ve afectada por las unidades de los valores originales de los datos y que están estandarizados.
Tomando el planteo de Hotelling, la variabilidad será máxima cuando el vector de cargas (vector que tiene los valores de los autovalores de la componente principal) es el autovector asociado al mayor autovalor de la matriz de varianza y covarianza.
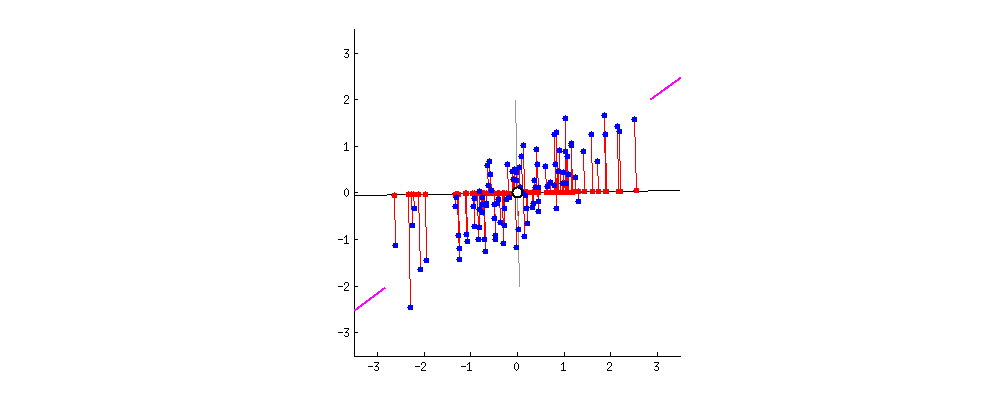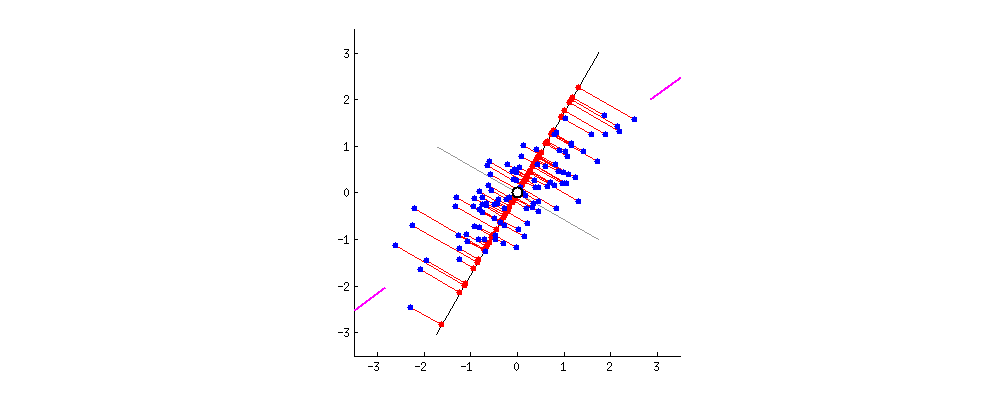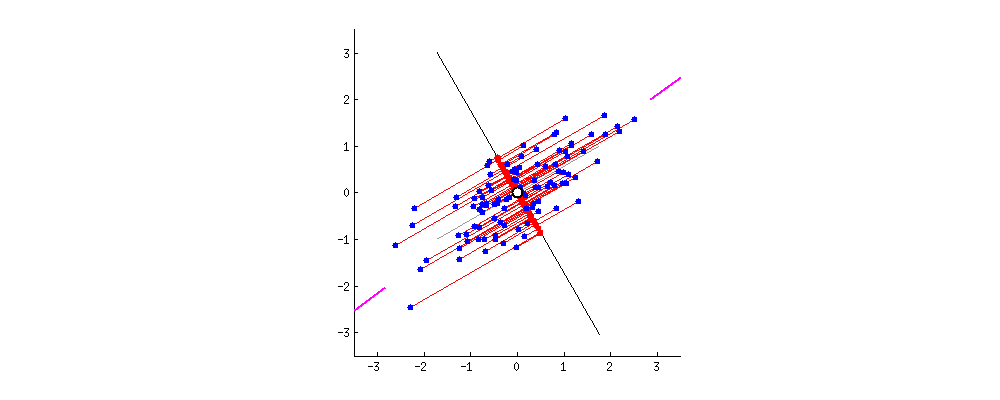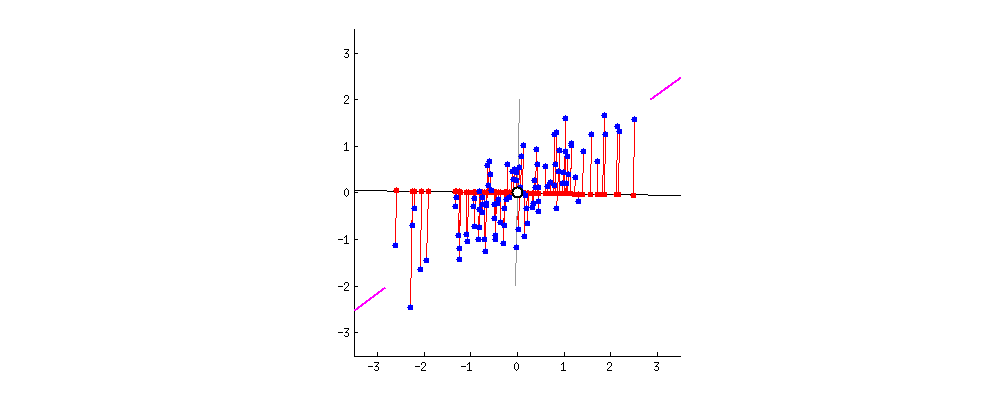
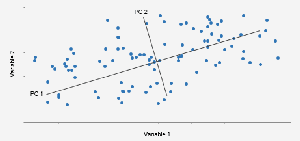
El gráfico animado muestra cómo al aplicar una transformación, los ejes van rotando y cómo la proyección de los puntos sobre los mismos tiene, en algunos casos, poca variación (rango de valores) y cuando se alinea sobre la dirección de la nube de puntos, es máxima sobre el nuevo eje x. Allí es donde tiene una varianza máxima y el eje x tiene mayor capacidad de discernir/separar entre distintos puntos.
Los componentes principales son de la forma
Yi = Σ aij Xj = ai1X1 + ai2X2 + … aip Xp
Donde ||a1|| = 1. Convexa. Los coeficientes a son los loadings
L matriz deja a los autovalores en la diagonal por lo que lo que explica cada loading que es uno de los autovalores, es el autovalor sobre la traza de la matriz que es la suma de todos los autovalores. Los autovalores son positivos y decrecen en valor en la medida en que avanzan. Es así que se puede hacer la cuenta de con cuántos de ellos se puede explicar un porcentaje determinado de la varianza total. Si las variables no tienen correlación alguna entre sí, los autovalores tendrán un valor muy similar entre ellos y no tendrá sentido hacer análisis de componentes principales.
Criterios de cantidad de valores a tomar
% a explicar: se define un factor q será el porcentaje a explicar y tendrá que ser menor a la suma de los % de los valores tomados.
Kaiser: Si los valores son > 1, explican más que la variable original. Entonces nos quedaremos con los > 1, aunque algunos autores recomiendan 0.7 según estudios con simulaciones de Montecarlo.
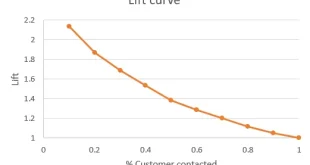
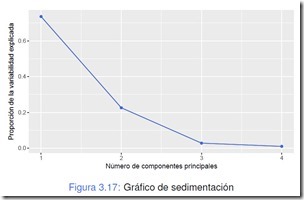
Bastón Roto: Se toman tantas componentes hasta que el “bastón se corta” en el gráfico de sedimentación scree. de % de explicación de la variabilidad en función de la cantidad de componentes.
Test secuencial basado en chi cuadrado. Se toman tantas como hagan falta para dejar las que quedan esféricas, es decir, de más o menos el mismo valor. No se usa mucho y se recomienda cuando el número de observaciones sobre el de variables sea menor a 5 porque sino el test rechaza siempre por tratarse de una muestra muy grande.
Se trabaja con la matriz de correlación, no la de covarianza (además está normalizada?)
La importancia de la escala, el centrado y cuántos PCAs se pueden esperar
PCA con lenguaje R
Más sobre Machine Learning
