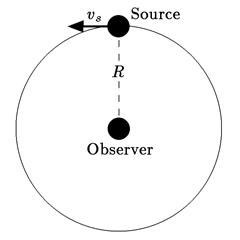
 Considerar el corrimiento Doppler para un observador estático de un objeto que se desplaza en órbita circular de radio R alrededor del mismo a una velocidad tangencial Vs.
Considerar el corrimiento Doppler para un observador estático de un objeto que se desplaza en órbita circular de radio R alrededor del mismo a una velocidad tangencial Vs.
a) Si la onda en cuestión es sonido y Vs es pequeña respecto de c, cuál será el corrimiento Doppler z?
La velocidad relativa del objeto y del observador es 0, es decir, la distancia entre ellos no varía, por otro lado, a velocidades no relativistas, los relojes están sincronizados por lo que los intervalos de tiempo son los mismos y el corrimiento resulta cero.
![]()
b) En el caso en que la onda sea luz viajando a velocidad c, y Vs no es pequeña respecto de c, hay que tomar en consideración la dilación temporal donde el reloj del objeto en movimiento transcurre más lento según:
![]()
Si los intervalos de tiempo entre crestas se miden como ∆ts, entonces para el observador parecerán como γ.∆ts
![]()
 Solo para Entendidos
Solo para Entendidos