GeoJSON Right Hand Rule Fix in Python

Qué es el right hand rule?

El “right hand rule” (regla de la mano derecha) en GeoJSON se refiere a una convención para ordenar las coordenadas de los polígonos en un archivo GeoJSON. Según la especificación GeoJSON (RFC 7946), los polígonos deben seguir la regla de la mano derecha para garantizar la interoperabilidad entre diferentes sistemas y aplicaciones.

La regla de la mano derecha establece que, al recorrer las coordenadas de un polígono en sentido horario, el área encerrada se considera “exterior” del polígono. Por otro lado, al recorrer las coordenadas en sentido antihorario, el área encerrada se considera “interior” del polígono. En otras palabras, los anillos exteriores de los polígonos deben tener coordenadas en sentido horario, mientras que los anillos interiores (agujeros) deben tener coordenadas en sentido antihorario.

Esta convención es importante para evitar ambigüedades al procesar y representar los datos geográficos. Al seguir la regla de la mano derecha, los sistemas y aplicaciones que trabajan con archivos GeoJSON pueden interpretar correctamente cuál es el interior y el exterior de los polígonos, lo que resulta en un procesamiento y visualización más precisos de los datos.

Código en Python

from typing import List
import math

def reorder_polygon(polygon: List[List[float]]) -> List[List[float]]:
    # Calcular el centroide del polígono
    centroid = [sum(x) / len(x) for x in zip(*polygon)]
    
    # Definir una función para calcular el ángulo entre dos vectores
    def angle_between_vectors(u, v):
        dot = u[0]*v[0] + u[1]*v[1]  # Producto escalar de u y v
        det = u[0]*v[1] - u[1]*v[0]  # Determinante de u y v
        return math.atan2(det, dot)  # Calcular el ángulo entre u y v usando atan2
    
    # Ordenar los vértices en función del ángulo que forman con el centroide
    sorted_polygon = sorted(polygon, key=lambda x: angle_between_vectors([1, 0], [x[0] - centroid[0], x[1] - centroid[1]]))
    
    return sorted_polygon

1. Se importan los módulos List de typing y math para usar sus funciones y definiciones de tipos.

2. La función reorder_polygon toma como entrada un polígono representado como una lista de vértices (coordenadas [x, y]).

3. Se calcula el centroide del polígono sumando las coordenadas x y y de cada vértice y dividiendo por el número de vértices.

4. Se define una función anidada llamada angle_between_vectors que toma dos vectores u y v como entrada y devuelve el ángulo entre ellos.
– Primero, se calcula el producto escalar (dot) y el determinante (det) de los dos vectores.
– Luego, se utiliza la función math.atan2 para calcular el ángulo entre los dos vectores.

5. Se ordenan los vértices del polígono en función del ángulo que forman con el centroide.
– La función sorted ordena los vértices según la clave proporcionada.
– La clave es el ángulo entre el vector [1, 0] (representa el eje x positivo) y el vector que va desde el centroide al vértice actual.

6. La función devuelve el polígono con sus vértices ordenados en sentido horario.

Aquí un ejemplo de cómo llamar a la función y su salida.

# Crear un polígono de ejemplo (vértices no ordenados)
polygon = [
    [2, 2],
    [4, 4],
    [6, 2],
    [4, 1]
]

# Utilizar la función reorder_polygon para ordenar los vértices en sentido horario
sorted_polygon = reorder_polygon(polygon)

print("Polígono original:", polygon)
print("Polígono ordenado:", sorted_polygon)

Polígono original: [[2, 2], [4, 4], [6, 2], [4, 1]]
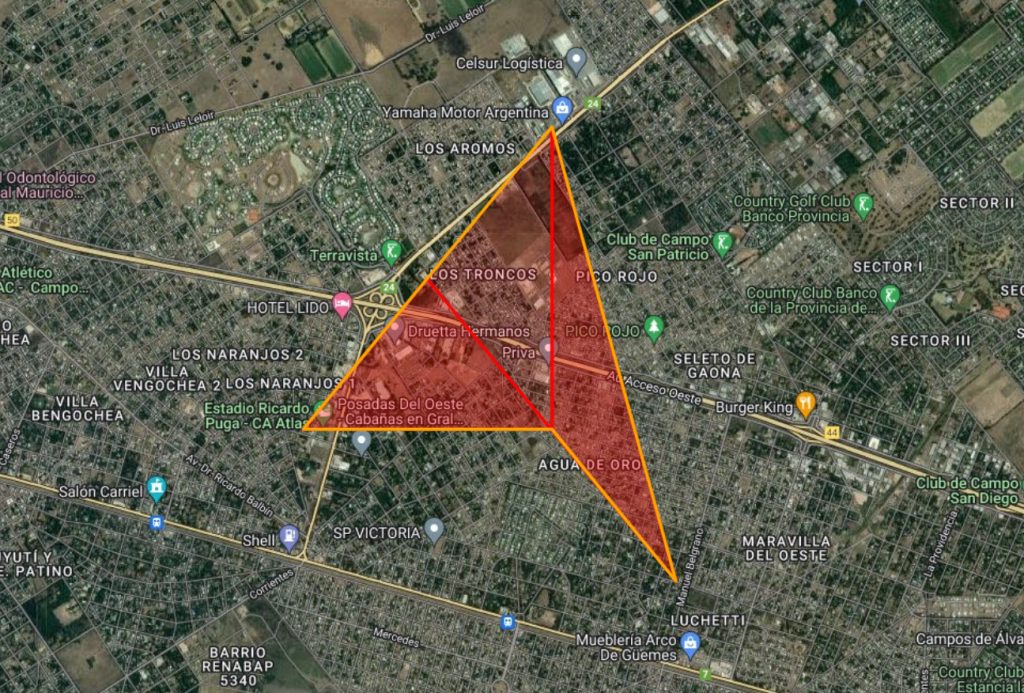
Polígono ordenado: [[6, 2], [4, 4], [2, 2], [4, 1]]

Aquí se ve en folium cómo el orden incorrecto hace que la superficie roja no conforme un polígono regular y al ordenar los puntos mediante la regla de la mano derecha, se logra el polígono naranja.