Solo para Entendidos
Related Articles
En muchas estrellas se han observado picos de emisión en el espectro infrarrojo que llevan a pensar en otros objetos en sus inmediaciones. Es el ejemplo de Vega α Lyr
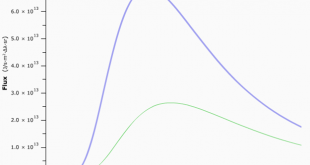
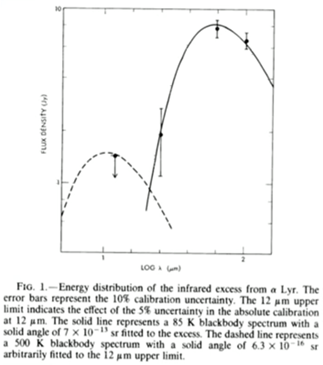
En este gráfico se ve a la izquierda el espectro visible que cae en la zona del infrarrojo. A la derecha, exagerado, el espectro infrarrojo que no se explica simplemente por la estrella. La luminosidad de la estrella en el infrarrojo es de 2.5 10-5 Lvega. Una fracción del espectro visible pero lo suficientemente notable.
Este exceso en el espectro infrarrojo nos lleva a suponer otro objeto en las cercanías de la estrella.
Por la ley de Wien. λmax = b/T resulta
\(T = \frac{b}{ \lambda_m}\)En este caso, para λ = 60 μm,
\(T \simeq 50ºK\)Por otro lado la estimación de la temperatura de un cuerpo oscuro se da según la siguiente ecuación de donde se puede deducir la distancia a la estrella. Donde σ es la constante de boltzman. Lvega= 3.8 1026 W.
\(T=\sqrt[4]{\frac{L}{16 \pi \sigma D^2}} \simeq 50ºK\) \(D=\sqrt{\frac{L}{16 \pi \sigma T^4}} \simeq 200 AU\)Así, la superficie del objeto, para que irradie lo recibido por la estrella en esa frecuencia, debe cumplir con:
\(L=\frac{\pi r^2}{4 \pi D^2}\) entonces \(r = \sqrt{2.5 *10^5 *4 *D^2} = 2.9 10^{11} m\)Resulta un tamaño ridículo para un objeto por lo que se entiende que se trata de un campo de desechos que forma un disco alrededor de la estrella.
En la medida en que la masa se divide en pequeñas partículas, la fracción de radiación reflejada sobre la superficie de las partículas se da conforme a:
\(Area = \frac{n*r^2}{4*D^2}\)Si distribuimos una masa M con sierta densidad:
\(\frac{3*M}{4*r*\rho} \propto \frac1r\)