Relativity Draft

Events: something that happens instantaneously at a single point in spacetime, such as a light flashing, or a point on a moving object passing another point. All events in spacetime are defined using the four coordinates t, x, y, z. Imagine a particle moving through spacetime as a succession of events through spacetime, the line linking all those events is called the particle’s world-line.

Frame of Reference: The coordinate system from which each observer takes measurements.

The two Postulates of Special Relativity:

• The laws of physics are the same in any inertial frame of reference, regardless of position or velocity.
• The constancy of the speed of light in a vacuum – the speed of light in vacuum has the same value c = 3 × 108 m s-1 in all inertial frames of reference.

Vertical axis is ct –not t- in order to draw the world-line of light at 45º (convenient scale).

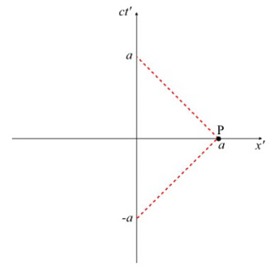
To add a second observer we will define a S’ as a new frame of reference. The speed of light c is the same for all inertial observers. This means that any light ray will always be drawn with a 45° slope for any inertial frame. The broken line represents a light ray emitted at x’ = 0, ct’ = -a, striking a mirror at x’ = a, ct’ = 0 and reflected back to x’ = 0, ct’ = a. We call the point (or event) P where x’ = a, ct’ = 0.

As a varies, so will the position of point P. In fact, because of the constancy of the speed of light, point P (where ct’ always equals zero) traces out the x’ axis for different values of a.

 

 

 

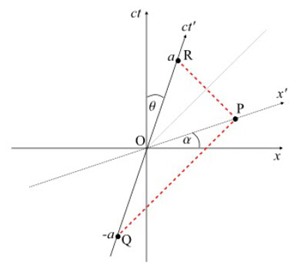
We use this property of point P to define the position of the x’ axis in Figure at the right. This time we are back to showing the reference frame S of observer O, who records a light ray (the broken line) emitted at point Q (x’ = 0, ct’ = -a) striking a mirror at point P (x’ = a, ct’ = 0) and reflected back to point R (x’ = 0, ct’ = a). The broken lines from points Q and R must be at 45° to the x axis. Where these lines intersect must be at point P, the position of the mirror at x’ = a, ct’ = 0. Therefore, a straight line drawn through P and the origin must define the x’ axis.

The triangle ORP is an isosceles triangle (two sides of equal length, and therefore two equal angles) bisected by a line at 45° to the x axis and passing
through O. Therefore, the x’ axis must make the same angle with the x axis as the ct’ axis makes with the ct axis, ie . θ = α

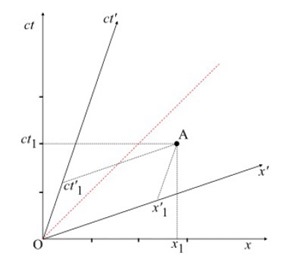How do we now describe the coordinates of a particular event A?
We need to construct coordinate lines parallel to the respective axes. We read off A’s coordinates with respect to the x and ct axes normally, as we would on any Cartesian grid.

We then construct a line passing through A and parallel to the x’ axis. Where this line crosses the ct’
axis gives us the ct’ coordinate – . Similarly, we then construct a line passing through A and parallel to the ct’ axis. Where this line crosses the x’ axis give us the x’ coordinate – .

 

TIME DILATION

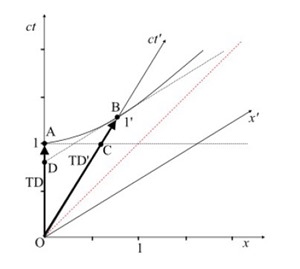Invariant hyperbola pass through the ct axis at ct = 1, and the ct’ axis at ct’ = 1.

The horizontal dotted line AC is a line of simultaneity for observer O, all events have the same time value of ct = 1.

The sloping dotted line BD (tangent to the hyperbola at B) is a line of simultaneity for observer O’, all events have time value of ct’ = 1.

Observer O’ measures event C occurring at a time ct’ < 1 on his ct’ axis. However, observer O measures the same event occurring at time ct = 1 on his ct axis.

From the point of view of O, the clocks on frame S’ belonging to O’ are running slow. The black arrow TD is the time dilation observed by O. Observer O measures event D occurring at a time ct < 1 on his ct axis. However, observer O’ measures the same event occurring at time ct = 1