Solo para Entendidos
Related Articles
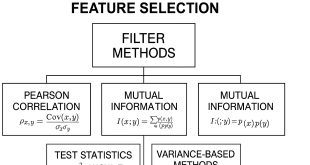
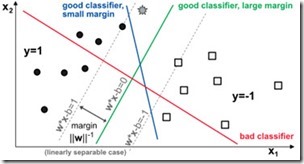
El algoritmo SVM (Support Vector Machine) es un método de aprendizaje supervisado utilizado para la clasificación y regresión de datos. El objetivo principal de SVM es encontrar el hiperplano de decisión que mejor separe las clases en un espacio de características de alta dimensión. El hiperplano de decisión es un límite que separa dos clases de datos y se calcula maximizando la distancia entre el hiperplano y los puntos de datos más cercanos de cada clase, llamados vectores de soporte.
El algoritmo SVM Support Vector Machine funciona de la siguiente manera:
-
Preprocesamiento de datos: Se realiza el preprocesamiento de datos para eliminar cualquier ruido, valores atípicos y datos faltantes. Luego se realiza la normalización o estandarización de datos para que todas las características tengan la misma escala.
-
Selección de características: Se seleccionan las características relevantes para el problema. La selección de características puede mejorar la precisión y eficiencia del modelo.
-
Creación del modelo SVM: Se crea un modelo SVM utilizando el conjunto de datos de entrenamiento. El modelo SVM encuentra el hiperplano de decisión que mejor separa las clases. El hiperplano se define como la frontera de decisión entre las dos clases. El modelo SVM también determina los vectores de soporte, que son los puntos de datos más cercanos al hiperplano.
-
Ajuste de parámetros: Se ajustan los parámetros del modelo SVM para maximizar la precisión del modelo. Los parámetros más importantes son C, que controla la penalización por errores de clasificación, y el kernel, que define la forma del hiperplano.
-
Predicción de clases: Se utiliza el modelo SVM para predecir las clases de los datos de prueba. Los datos de prueba se clasifican en función de su posición con respecto al hiperplano de decisión.
Algunas ventajas del algoritmo SVM son:
-
Es efectivo en espacios de alta dimensión.
-
Es eficiente en el uso de memoria.
-
Es versátil, ya que permite el uso de diferentes kernels para separar las clases.
Sin embargo, algunas desventajas del algoritmo SVM son:
-
Puede ser difícil de interpretar.
-
Requiere una selección cuidadosa de los parámetros para evitar el sobreajuste o subajuste del modelo.
-
Puede ser lento en el entrenamiento de grandes conjuntos de datos.
El SVM utiliza un conjunto de vectores de soporte para determinar la frontera de decisión, que es el límite entre las dos clases. Estos vectores de soporte son los puntos de datos que están más cerca de la frontera de decisión y son fundamentales para la construcción del modelo.
El objetivo principal del SVM es encontrar el hiperplano de separación que maximice la distancia entre las clases. Esta distancia se conoce como margen y se define como la distancia entre el hiperplano y los vectores de soporte más cercanos.
En el caso de problemas no lineales, el SVM utiliza una técnica llamada kernel trick, que permite transformar el espacio de características original a un espacio de características de mayor dimensión, donde los datos son separables linealmente. El kernel trick es esencialmente una forma de evitar el cálculo explícito de las coordenadas de los puntos en el espacio de características de mayor dimensión.
Para construir un modelo SVM, primero se debe seleccionar el tipo de kernel y los parámetros correspondientes. Los tipos de kernel más comunes son el lineal, el polinómico y el radial basis function (RBF). El parámetro C controla el grado de penalización por la violación de la margen, mientras que el parámetro gamma controla la forma de la función kernel en el caso del kernel RBF.
Una vez que se han seleccionado el kernel y los parámetros, se entrena el modelo utilizando un conjunto de datos de entrenamiento. Durante el entrenamiento, el modelo encuentra el hiperplano de separación óptimo que maximiza la distancia entre las clases y minimiza el error de clasificación.
Una vez entrenado el modelo, se puede utilizar para clasificar nuevos puntos de datos. El modelo asigna una clase a cada punto de datos en función de su posición en relación con la frontera de decisión. Si un punto se encuentra en un lado de la frontera de decisión, se clasifica como perteneciente a una clase, y si se encuentra en el otro lado, se clasifica como perteneciente a la otra clase.
Una de las principales ventajas de este modelo es que puede manejar fácilmente datasets que tienen una alta dimensionalidad, ya que su capacidad de generalización no se ve afectada por ello. Además, también es muy eficaz cuando se trabaja con datos que tienen un gran número de características.
Para ajustar los parámetros del modelo SVM Support Vector Machine, se utiliza una técnica conocida como “kernel trick“. Básicamente, esta técnica permite mapear los datos originales a un espacio de mayor dimensión, donde los datos se vuelven más fáciles de separar linealmente. De esta manera, incluso si los datos originales no son separables linealmente, todavía es posible encontrar un hiperplano que los separe de manera óptima en el nuevo espacio.
La elección del kernel es importante, ya que determina cómo se lleva a cabo la transformación de los datos. Los kernels más comunes son el kernel lineal, el kernel polinomial y el kernel radial (también conocido como kernel gaussiano). Cada uno de ellos tiene sus propias características y es más adecuado para ciertos tipos de datos.
Una vez que se ha seleccionado el kernel, el modelo SVM Support Vector Machine busca el hiperplano que mejor separa las dos clases en el espacio de mayor dimensión. Esto se hace maximizando la distancia entre el hiperplano y los puntos de datos más cercanos a él, también conocidos como vectores de soporte. Cuanto mayor sea la distancia entre el hiperplano y los vectores de soporte, mejor será la capacidad del modelo para generalizar a nuevos datos.
Finalmente, el algoritmo SVM es un modelo de aprendizaje supervisado muy potente y versátil que se puede utilizar para resolver una amplia variedad de problemas de clasificación y regresión. Su capacidad de manejar datasets con alta dimensionalidad y datos no lineales lo convierte en una herramienta muy útil en el campo del machine learning.
Kernel lineal: El kernel lineal es el más sencillo de los kernels y se utiliza para casos en los que se tiene una clara separación lineal entre las clases. Este kernel transforma los datos a un espacio de mayor dimensionalidad mediante una función lineal y se puede representar de la siguiente manera: K(x, y) = x^T y + c, donde x e y son los vectores de características de dos puntos en el espacio original, c es una constante y T representa la transposición. En este kernel, la función de decisión del clasificador es una línea recta que separa las clases.
Kernel polinomial: El kernel polinomial se utiliza cuando no se tiene una separación lineal clara entre las clases y se desea transformar los datos a un espacio de mayor dimensionalidad mediante una función polinomial. Este kernel se puede representar de la siguiente manera: K(x, y) = (x^T y + c)^d, donde d es el grado del polinomio y c es una constante. En este kernel, la función de decisión del clasificador es una curva de grado d que separa las clases.
Kernel radial: El RBF (Radial Basis Function) tiene la forma:
K(x_i, x_j) = exp(-gamma * ||x_i – x_j||^2)
Donde x_i y x_j son dos puntos en el espacio de características, ||.|| es la norma euclidiana, y gamma es un parámetro de ajuste que controla la forma de la función. Cuando gamma es grande, la función RBF es más estrecha y los puntos tienen que estar muy cerca para que el resultado sea significativo. Cuando gamma es pequeño, la función RBF es más amplia y los puntos pueden estar más alejados y aun así tener un impacto en el resultado.
El uso de la función RBF permite modelar superficies de decisión no lineales en el espacio de características. Esta técnica es útil cuando los datos no son linealmente separables en el espacio original, pero se pueden separar en un espacio de características de mayor dimensión.
El proceso de entrenamiento de SVM Support Vector Machine con la función de kernel RBF implica la selección de un conjunto de vectores de soporte que se encuentran en el límite de la región de decisión. El objetivo es maximizar la distancia entre los vectores de soporte y la superficie de decisión, lo que se conoce como margen. La selección de los vectores de soporte y el ajuste del valor de gamma se realizan mediante técnicas de optimización, como el descenso por gradiente.
Una vez que se entrena el modelo, se puede usar para hacer predicciones sobre nuevos datos. El proceso de predicción implica la proyección de los nuevos datos en el espacio de características y la clasificación según la ubicación con relación a la superficie de decisión.
