Solo para Entendidos
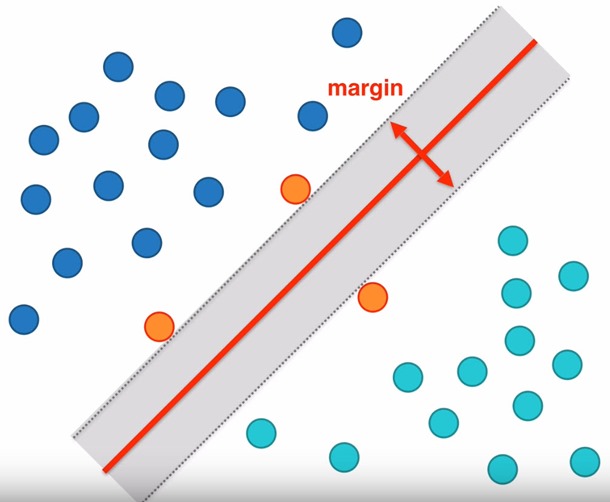
Si pensamos en separar estos dos grupos, vemos como la línea que mejor lo hace a la que logra el camino más ancho entre ellos. Es decir, el margen más grande logrado por el hiperplano (línea en rojo) según los support vectors. Para maximizar el margen, estudiaremos el problema como una optimización con restricciones que se resuelve mediante multiplicadores de Lagrange.
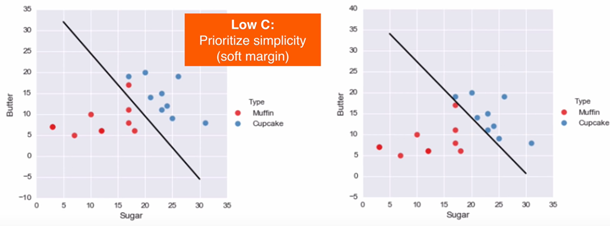
En los casos en que una línea recta no se ajuste, el modelo SVM tiene un parámetro C que regula la penalización de esa falla de clasificación. Con valores bajos de C, el modelo es más permisivo y logra márgenes suaves; con valores de C altos, es más estricto dejando márgenes más pequeños y aumentando la posibilidad de overfitting.
En varias dimensiones podemos encontrarnos con casos en que una línea no separa correctamente grupos de datos y un plano no es claramente la solución. Python dispone de diferentes kernels que pueden resolver el problema. Para el Kernel = RBF (Radial Basis Function), este introduce dos parámetros más: C (ya explicado) y Gamma. Al igual que C, cuanto mayor es Gamma, más overfitting.
model = svm.SVC(kernel=’rbf’, C=1, gamma=2**-5)
